Ao se debruçar sobre padrões misteriosos e belas repetições no universo, muitas vezes surge uma constatação surpreendente: basta uma regra matemática singela para que o inesperado floresça. Uma fórmula relativamente simples, como f(x) = x² + c, está na base de estruturas visualmente espantosas e vastas regiões de comportamento imprevisível. Mas como isso acontece? E por que matemáticos e cientistas seguem intrigados tantas décadas depois?
Da simplicidade ao fabuloso: a gênese dos fractais
É difícil imaginar que uma expressão tão modesta quanto f(x) = x² + c guarde tamanha riqueza. Segundo os estudos do Instituto de Matemática da Unicamp, tudo começa com a escolha de um valor para x, chamado de semente, e a repetida aplicação da fórmula usando, a cada passo, o resultado anterior como nova entrada. O valor de c, então, determina um universo inteiro de possibilidades.
O que acontece quando a regra é aplicada de novo, e de novo, e mais uma vez? Essa é a essência das iterações, o motor oculto dos fractais, dos caos e do fascinante fenômeno chamado entropia.
Padrão nasce da repetição simples, caos surge do detalhe escondido.
Iteração: o passo-a-passo do inesperado
Para entender de fato como tudo se forma, basta considerar o seguinte processo:
- Escolhe-se um número inicial, x0.
- Calcula-se x1 = f(x0) = x0² + c.
- Em seguida, x2 = f(x1) = x1² + c.
- Repete-se o procedimento quantas vezes quiser.
Seguindo esses simples passos, números podem permanecer finitos, tender ao infinito ou formar cadeias ciclantes. A beleza, e o estranho, se manifestam a partir de uma escolha específica do parâmetro c.
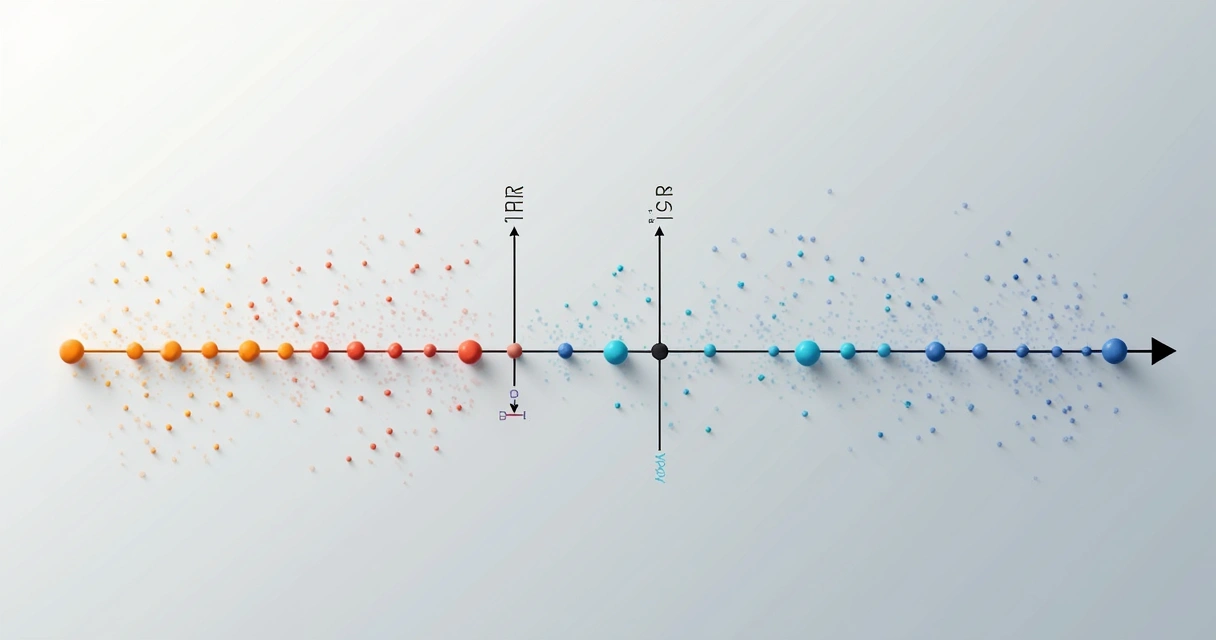
O Conjunto de Mandelbrot: limites, caos e beleza
O Conjunto de Mandelbrot, batizado em homenagem ao matemático Benoit Mandelbrot, tornou-se um ícone cultural tanto pela sua imagem quanto pela profundidade teórica. O conjunto, descrito em detalhes em estudo da USP, reúne todos os valores de c para os quais a sequência resultante da iteração permanece limitada, ou seja, nunca cresce sem parar.
Cada valor de c é, na verdade, como uma chave: alguns abrem portas para a regularidade, outros liberam o caos.
Quando o infinito aparece rapidamente
Pode-se até pensar que cada valor de c aponta para um resultado previsível, mas não é bem assim. Os matemáticos já sabem, por exemplo, que para c fora do intervalo de -2 a 1/4, a sequência rapidamente foge para o infinito. Uma conclusão relativamente fácil, demonstrada por métodos básicos de análise, mas dentro desse intervalo, a história muda de tom.
Dentro de intervalos curtos, cabe todo o mistério do infinito.
O que acontece quando c está entre –2 e 1/4?
Esse intervalo reúne c’s misteriosos. Há infinitos valores que ainda hoje desafiam o entendimento matemático: não se sabe se a sequência de iterações acabará formando um ciclo ou se mergulhará para sempre em comportamento caótico. Até mesmo para valores aparentemente simples, como c = –3/2, ainda pairam dúvidas fundamentais. Esse desconhecimento é ilustrado nos estudos da UFRGS.
Outros pontos dentro desse intervalo já tiveram seu comportamento classificado, seja como cíclico, regular, ou totalmente errático. Mas a imensidão do desconhecido persiste, e é fonte renovada de fascínio e pesquisa.

Frações, raízes e o poder dos números: dinâmica com c racional
Interessante reparar que, dentre todos esses números c possíveis, os racionais têm um charme único. Um resultado surpreendente foi demonstrado por Clayton Petsche e Chatchai Noytaptim: apenas três valores racionais, 0, –1 e –2, levam a ciclos periódicos. Ou seja, para estes valores de c, a sequência acabará entrando em um padrão que se repete indefinidamente após alguns passos iniciais.
Poucos números racionais abrigam o refúgio da ordem nesse mar de caos.
Por que só esses três?
A resposta passa pelo conceito de números totalmente reais, solução de equações polinomiais com coeficientes inteiros e todas as raízes reais. Esse grupo inclui todos os racionais, e certos irracionais, como a raiz quadrada de 2, mas exclui outros, como a raiz cúbica de 2, que possui raízes complexas.
Números totalmente reais: mais do que parece
Para visualizar melhor, veja:
- Números racionais: por exemplo, 1/3, -2, 0.
- Irracionais totalmente reais: √2, –√3, etc.
- Irracionais não totalmente reais: ³√2 (raiz cúbica), já que polinômios do tipo x³ - 2 = 0 possuem raízes complexas.
Ainda assim, apenas c = 0, –1, ou –2 fornecem, para qualquer semente inicial, um retorno ao ponto inicial após certo número de iterações. Mesmo cercados por infinitos outros números racionais, só esses três pavimentam o caminho da ordem completa.
Hipérboles, regularidade e caos: o avanço recente da matemática
Conforme o tempo avança, matemáticos como Misha Lyubich descobriram que, dentro do intervalo de –2 a 1/4, a maior parte dos valores de c exibe comportamento regular, chamado hiperbólico. De maneira independente, Jacek Graczyk e Grzegorz Swiatek confirmaram que, apesar da fama de caótico, o conjunto dos c irregulares (comportamento caótico) ali é raro em termos quantitativos.
Regularidade esconde-se sob o véu do extraordinariamente complexo.
E mais: Sebastian van Strien ampliou esses resultados, mostrando que, para grande parte das funções analíticas reais, padrões hiperbólicos dominam. Mesmo assim, o mar nunca é totalmente calmo: valores densos de caos persistem, pontuando a ordem e tornando o cenário dinâmico.

A exceção faz o padrão: ciclos parabólicos e raridade extrema
Se ciclos periódicos já são raros, os chamados ciclos parabólicos são quase unicórnios matemáticos. Xavier Buff e Sarah Koch mostraram que, ao considerar valores totalmente reais de c, apenas 1/4, –3/4, –5/4 e –7/4 geram tal comportamento especial. Aqui, a diferença reside na maneira como as órbitas se aproximam de seus ciclos, mais lentamente, deslizando na fronteira entre ordem e instabilidade.
Esses valores não só são escassos, mas desempenham papel determinante nas estruturas mais profundas do Conjunto de Mandelbrot. Operam como pontos de transição, marcando fronteiras entre ilhas de regularidade e oceanos de imprevisibilidade.
Raridade extrema: poucos números desenham linhas invisíveis no mapa dos fractais.
Galois, conjugados e portas para outro universo
A ponte entre dinâmica de iterações quadráticas e teoria dos números emerge de conceitos como os conjugados de Galois. Cada número totalmente real pode ser visto como um dos valores que satisfaz determinado polinômio com coeficientes inteiros. Seus "irmãos" ocultos, os conjugados, parecem ecoar o comportamento do valor original, desenhando padrões conjuntos.
William Thurston, pesquisando essas ligações, percebeu que, ao mapear a entropia topológica de quase um bilhão de valores reais de c e seus conjugados, surgia uma figura inesperada. Não era um ponto, nem uma linha. Era um objeto com aparência de rosquinha.
Bagel da entropia: fractal raro e elegante
Esse objeto ganhou o nome de bagel da entropia (ou entropy bagel). Trata-se de uma estrutura fractal, circular, mas com recortes minúsculos e padrões internos que desafiam explicação simples. Uma rosquinha, formada pela maneira como o grau de imprevisibilidade, a entropia, se distribui entre todos esses valores especiais de c.
Padrões fractais se reúnem num bagel: caos, ordem e arte, tudo junto.

Mas afinal, o que é entropia nesse contexto? Entropia mede a aleatoriedade: o quanto o comportamento do sistema pode ser previsto. Aqui, a entropia topológica traduz o grau de "bagunça" da dinâmica do polinômio ao longo das iterações para certos valores de c. Valores mais altos indicam mais imprevisibilidade.
Como o bagel da entropia aparece?
A formação desse curioso objeto passa pelo estudo das taxas de crescimento de órbitas das iterações, quantas sequências distintas podem surgir após certo número de passos. Ao se calcular essa medida para cada número totalmente real de c e todos os seus conjugados de Galois, o espectro da entropia desenha automaticamente uma rosquinha fragmentada e colorida: o bagel da entropia.
Ao contrário de muitos objetos matemáticos previsíveis, o bagel não surge de uma receita direta. Ele emerge, revelador, quando se olha para um imenso horizonte de comportamentos, todos organizados, paradoxalmente, por regras elementares.
Grandeza se esconde atrás da aparente simplicidade.
Padrão dentro do caos: lições do bagel da entropia
O bagel ilustra de maneira brilhante a principal descoberta dos fractais: a ordem pode se organizar mesmo do que parece puro acaso. Uma função simples, como x² + c, quando aplicada a quantidades imensas de números, conecta teoria dos números, caos, periodicidade e beleza visual.

Uma dança entre teoria dos números e sistemas dinâmicos
Para muitos matemáticos, o verdadeiro encanto está na interseção. Os sistemas dinâmicos, que descrevem como estados evoluem sob regras fixas, e a teoria dos números, sempre preocupada com propriedades profundas dos números racionais, inteiros e irracionais, conversam quando analisam fractais derivados de polinômios quadráticos.
A cada novo estudo, surge um vínculo antes invisível. Números ditos "simples" podem, quando vistos sob o prisma das iterações, mostrar comportamentos tão ricos quanto os números transcendentes, como π ou e. E nesses cruzamentos, fractais inesperados despontam, como o bagel da entropia.
Descobertas não cessam, pois sempre há um novo elo a ser desvelado.
Por que, afinal, matemáticos continuam impressionados?
- Mesmo as regras mais simples se mostram imprevisíveis após várias iterações.
- Números a princípio banais, como –3/2, continuam indecifrados.
- Padrões visuais de extrema beleza emergem espontaneamente de puras operações algébricas.
- Inovações recentes ampliaram enormemente a compreensão, mas o mistério persiste.
Fractais: arte, natureza e matemática unificados
A influência dos fractais não se restringe ao mundo dos matemáticos. Tais padrões se revelam em galáxias, nuvens, árvores, na forma dos rios e nos vasos sanguíneos do corpo humano. O estudo dessas formas, volume após volume, reforça uma percepção quase poética: há ordem no caos, e há caos em toda ordem.
Pessoas comuns, artistas, programadores e cientistas se sentem igualmente atraídos pelo apelo visual dessas estruturas. O bagel da entropia, quase desconhecido fora dos círculos científicos, captura esse espírito, mistura de rigidez matemática e estética imprevisível.

Conclusão
Os fractais nos mostram que a combinação de paciência e persistência matemática produz maravilhas quase inatingíveis pela imaginação comum. A simplicidade de uma fórmula como f(x) = x² + c revela um universo de complexidade, beleza e mistério. Do Conjunto de Mandelbrot ao bagel da entropia, as iterações de funções quadráticas desenham pontes entre a regularidade e o imprevisível.
Mesmo após décadas de pesquisa, fenômenos simples continuam surpreendendo, lembrando que o infinito cabe em cada intervalo, e que o inesperado pode estar oculto em qualquer regra despretensiosa. A busca por novas descobertas permanece aberta, alimentando o fascínio e a admiração por um universo matemático tão rigoroso quanto encantador.
Perguntas frequentes
O que é entropia nos fractais?
Entropia, no contexto dos fractais, é uma medida do quanto o comportamento do sistema é imprevisível ao longo das iterações. Mais especificamente, no estudo dos polinômios quadráticos como f(x) = x² + c, a entropia topológica indica a quantidade de desordem ou aleatoriedade presente nas sequências geradas. Quanto maior a entropia, mais difícil é prever como será o próximo termo da sequência apenas a partir do atual. No caso de fractais como o bagel da entropia, essa medida visualiza como padrões emergem e se organizam dentro do caos aparente.
Como o Mandelbrot descobriu os fractais?
Benoit Mandelbrot estudou como processos simples, quando repetidos, podiam criar imagens infinitamente complexas e autossimilares. Durante estudos em computação gráfica e matemática nos anos 1970, ele analisou comportamentos de funções complexas e percebeu que certos conjuntos de números, definidos por regras de iteração, produziam imagens com detalhe em todas as escalas. Mandelbrot popularizou o termo “fractais” e mostrou, com o auxílio de computadores, a beleza do conjunto que leva seu nome, como detalhado na apresentação do Instituto de Matemática da Unicamp.
Por que fractais são considerados caóticos?
Fractais são considerados caóticos porque pequenas diferenças nas condições iniciais podem provocar mudanças radicais no comportamento das sequências geradas. Essa sensibilidade implica que é virtualmente impossível prever os próximos passos sem conhecer precisamente todos os dados. Apesar desse caos local, há padrões globais e autossimilaridade, características que mantêm a beleza e a ordem mesmo diante da imprevisibilidade.
O que é o bagel da entropia?
O bagel da entropia é uma estrutura fractal descoberta ao mapear a quantidade de entropia (grau de aleatoriedade) para números totalmente reais de c e seus conjugados de Galois em funções como f(x) = x² + c. Ele se parece, visualmente, com uma rosquinha e representa, de forma gráfica, como a ordem e o caos se distribuem em todo o espectro desses valores.
Como criar fractais simples em casa?
Fractais simples podem ser criados com papel, lápis e uma calculadora, ou em programas de computador básicos. Basta definir uma regra, como x → x² + c, escolher um valor inicial e aplicar a fórmula repetidamente, anotando os resultados ou desenhando um gráfico. Ferramentas de desenho digital ou softwares gratuitos também permitem visualizar fractais complexos, como a árvore de Pitágoras ou conjuntos de Julia, usando apenas iterações e valores simples de c.



